How To Make A Camera Orbit A Character C# With A Mouse

Support me!

If you enjoy these webpages and you want to bear witness your gratitude, feel costless to support me in anyway!

Like Me On Facebook! Megabyte Softworks Facebook

Like Me On Facebook! Megabyte Softworks Patreon

026.) Camera Pt.3 - Orbit Camera

<< back to OpenGL 4 serial

Hi friends! I'thou really glad that you stumbled upon my 26th tutorial of my OpenGL 4 series, where yous can learn about the orbit photographic camera! In comparison with previous tutorial about transform feedback particle organisation, this tutorial is going to be a lot easier and much more relaxing . Just go on reading and y'all volition see, that it'southward really a slice of cake .

What is orbit camera

Orbit photographic camera (also known equally arcball camera) is a simple type of camera, that orbits around the object (like a planet) along a sphere. The simplicity of this camera is, that the view point is always the center of the sphere and the center is merely floating effectually the sphere. In lodge to move around the sphere, we accept to empathize the spherical coordinates. And for easier agreement, let's start with simpler 2D version - polar coordinates.

Polar coordinates

In 2D, we can represent a position in space with [x, y] coordinates. That'south simple, just there is an alternative way how to correspond position in infinite as well - with radius and angle. If you imagine the whole space as an infinitely big circle, then you tin correspond all positions as well! Look at the pic:

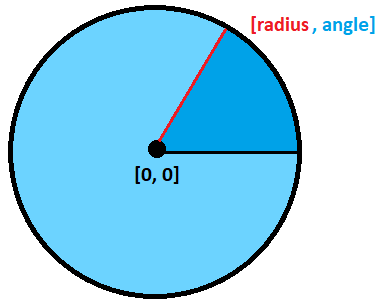
That means basically, that to reach our position, we first plow effectually past the specified bending and and then travel the radius distance! I call back the concept is really not that difficult to grasp. I also take a feeling that now you lot start to guess, what are spherical coordinates. Yes, information technology'south simply natural extension of this to 3D infinite .

Spherical coordinates

Now that we are in 3D, we can again ascertain a position autonomously from [x, y, z] coordinates in a like fashion as with polar coordinates, but this time, we will demand 2 angles instead of i - azimuth angle and polar bending. The azimuth bending is the rotation angle around Y axis, so with azimuth we control looking to the left and right, polar angle is for looking up and down . Accept a wait at the picture once more:

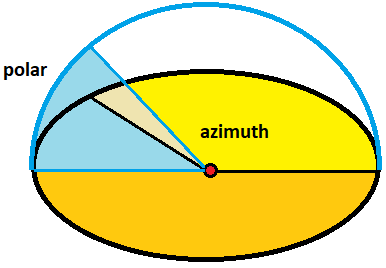
But why exactly do we demand those coordinates? Considering that'due south how we can implement the orbit camera easily! All nosotros need to do is to control those three parameters - radius (which is also a zoom level), azimuth angle and finally the polar bending! Having all iii parameters, all that remains is to summate the real [ten, y, z] position and that's it - nosotros accept the center position of the camera! Remember, the view indicate is always center of the sphere, then all we need is to calculate the eye of the camera, that orbits around the sphere .

And then the real question is - how tin we convert from polar coordinates to standard 3D coordinates? I didn't come up with it, it's but everywhere to be plant on the net. Simply converted to my namings and angles, here is the equation:

Given sphere with center signal c and [a, p, r], where:

a - azimuth angle
p - polar bending
r - radius

Then corresponding [ten, y, z] coordinates are:

10 = c.10 + r*cos(p)*cos(a)
y = c.y + r*sin(p)
z = c.z + r*cos(p)*sin(a)

Now that nosotros know the whole theory, let's take a look at the code .

Implementation

Beneath is the overview of the whole OrbitCamera class:

          class OrbitCamera { public: 	OrbitCamera(const glm::vec3& eye, const glm::vec3& upVector, bladder radius, bladder minRadius, float azimuthAngle, bladder polarAngle);      void rotateAzimuth(const float radians);     void rotatePolar(const float radians); 	void zoom(const bladder by);  	void moveHorizontal(const bladder distance); 	void moveVertical(const float distance);      glm::mat4 getViewMatrix() const;     glm::vec3 getEye() const;     glm::vec3 getViewPoint() const;     glm::vec3 getUpVector() const;     glm::vec3 getNormalizedViewVector() const;     float getAzimuthAngle() const;     float getPolarAngle() const;     float getRadius() const;  private:     glm::vec3 center_; // Center of the orbit camera sphere (the bespeak upon which the camera looks)     glm::vec3 upVector_; // Up vector of the camera     float radius_; // Radius of the orbit camera sphere     float _minRadius; // Minimal radius of the orbit camera sphere (cannot fall below this value)     float azimuthAngle_; // Azimuth angle on the orbit camera sphere     float polarAngle_; // Polar angle on the orbit camera sphere };

I really think that the namings of methods / variables should be mostly self-explanatory. Nevertheless, permit'due south analyze few core functions .

rotateAzimuth

          void OrbitCamera::rotateAzimuth(const float radians) {     azimuthAngle_ += radians;      // Go on azimuth angle within range <0..2PI) - information technology's not necessary, only to accept it nicely output     const auto fullCircle = 2.0f*glm::pi();     azimuthAngle_ = fmodf(azimuthAngle_, fullCircle);     if (azimuthAngle_ < 0.0f) {         azimuthAngle_ = fullCircle + azimuthAngle_;     } }

Here we rotate azimuth angle. The bending is free to become in a full circle, the just extra matter I exercise here is keeping the bending within the range 0 ... 2PI. This is done past role fmod. Information technology'due south similar a standard integer mod, but for floats. Should nosotros get beneath 0.0f, so the fmod returns negative value, that's why nosotros need to add it to the full circle .

And why exactly exercise I go along the angle in this range? One reason is a nice output of angle in the HUD (it'south easier to imagine 0 ... 360 degrees than 53531 degrees ), another is, that if we would rotate many many times effectually and the float value would go very high (or very low), we would kickoff losing precision, which could pb to unexpected results. Question is who would be patient plenty to rotate so much that he bumps into floating point precision problems .

rotatePolar

          void OrbitCamera::rotatePolar(const float radians) {     polarAngle_ += radians;      // Cheque if the angle hasn't exceeded quarter of a circle to forestall flip, add a fleck of epsilon similar 0.001 radians     const auto polarCap = glm::pi() / 2.0f - 0.001f;     if (polarAngle_ > polarCap) {         polarAngle_ = polarCap;     }      if (polarAngle_ < -polarCap) {         polarAngle_ = -polarCap;     } }

Here nosotros rotate polar angle. Nevertheless, we restrict this angle to go upwardly to quarter of a circle (PI / 2). But why y'all may enquire? Because if we don't do that, the camera will flip effectually when you exceed the quarter circumvolve (meet it for yourself by commenting those conditions out). The principal problem here is, that after exceeding this, you are not looking like forwards anymore, your're looking astern from now on. I haven't figured out all the same, how to make a perfect camera (like one in Blender software), but I surely volition research this and write a tutorial later .

Why is at that place a chip of epsilon? Considering this way nosotros won't reach full quarter of circumvolve. If nosotros exercise, then upward vector and view vector would become collinear and I suppose it would non piece of work properly anymore.

zoom

          void OrbitCamera::zoom(const float past) {     radius_ -= past;     if (radius_ < _minRadius) {         radius_ = _minRadius;     } }

This is pretty like shooting fish in a barrel - we're just manipulating the radius. If the radius falls beneath the minimal radius, we just cap it .

getEye

          glm::vec3 OrbitCamera::getEye() const {     // Calculate sines / cosines of angles     const auto sineAzimuth = sin(azimuthAngle_);     const auto cosineAzimuth = cos(azimuthAngle_);     const auto sinePolar = sin(polarAngle_);     const auto cosinePolar = cos(polarAngle_);      // Summate eye position out of them     const auto x = center_.x + radius_ * cosinePolar * cosineAzimuth;     const auto y = center_.y + radius_ * sinePolar;     const auto z = center_.z + radius_ * cosinePolar * sineAzimuth;      render glm::vec3(x, y, z); }

This i is actually important, considering it'due south the cadre code of the orbit camera. Here, the azimuth angle, polar angle and radius become translated into the position using the equation stated higher up. This code is simply implementation of the equation .

moveHorizontal / moveVertical

          void OrbitCamera::moveHorizontal(const float distance) {     const motorcar position = getEye();     const glm::vec3 viewVector = getNormalizedViewVector();     const glm::vec3 strafeVector = glm::normalize(glm::cross(viewVector, upVector_));     center_ += strafeVector * distance; }  void OrbitCamera::moveVertical(const float distance) {     center_ += upVector_ * altitude; }

With those functions we can motion the camera around (moving the eye of orbit camera sphere). Moving horizontally utilizes aforementioned logic for strafing as in the 006.) Camera Pt.two - Flying Camera and moving vertically is simply sliding along up vector .

Remainder of the functions are non really worth explaining, they are just getters with lilliputian to no logic .

Wireframe mode

In this tutorial, you lot can plow the wireframe manner on / off with the 'X' push. How to implement this on OpenGL? Information technology's really simple - y'all only have to call one OpenGL method prior to the rendering. In social club to return wireframe, phone call following method:

          glPolygonMode(GL_FRONT_AND_BACK, GL_LINE);

And to restore normal rendering mode, call post-obit method:

          glPolygonMode(GL_FRONT_AND_BACK, GL_FILL);

Consequence

The consequence is following scene showing 4 primitives - torus, cube, cylinder and sphere, which you can observe with our orbit camera (utilize mouse to control it - LMB to rotate, MMB to move effectually):

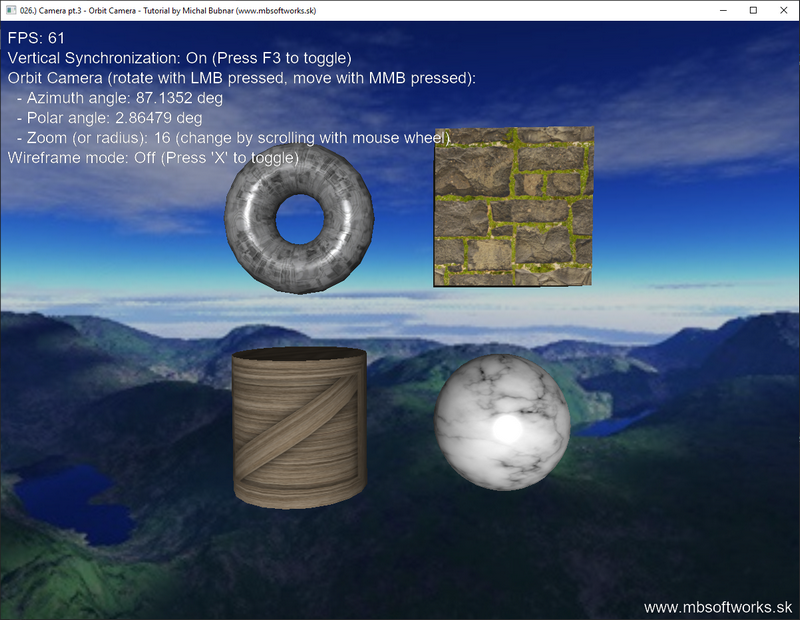
So equally you see - today we've accomplished something very nice and in the end it was not that difficult . I think it's a really nice add-on to our armory of cameras, we now accept 3 already! I think there will once be last camera tutorial, that allows you lot to rotate freely in every direction, something similar a space flight simulator .

Download 3.71 MB (359 downloads)